

In the case of more complex situations, the above equation is even more disputable. The damage is the same regardless of the probability you may conjure up. So, if you get caught by radar, the cost is 100 Euros if p=0.1, or 0.001 or even 0.0000001.
For you, statistics begin the moment you start the engine. If YOU get caught, you get caught independently of the probability suggested by past statistics. In this simple example, the cost was easy to estimate.
#Ffx hi risk probability drivers#
Try arguing with a policeman that your fine should be 10 Euros! Suppose that drivers are obliged to carry on board a regulatory capital for fines (something similar to Basel II or III). In other words, if you drive fast, you’re risking a 100 Euros note, not a 10 Euros one. If you get caught, you pay 100 Euros, if you don’t, you pay nothing. The above formula would suggest that anyone who is speeding is risking 1/10 X 100 = 10 Euros.
#Ffx hi risk probability driver#
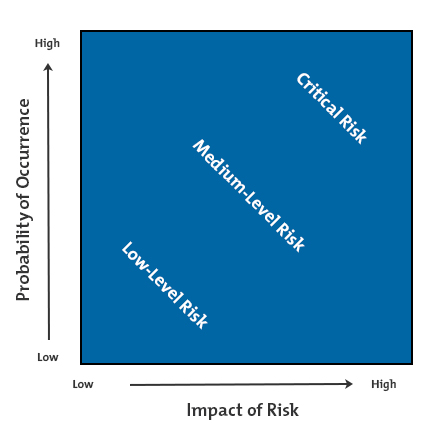
It is known from statistics that on that portion of the motorway on average one driver out of ten gets caught. If you’re 20-30 km/h above the limit, you can expect a fine of around 100 Euros. Suppose that in a certain portion of a motorway a radar is mounted with the intent of catching those who enjoy speeding. very rare events with dramatic consequences). Imagine the following example which was discussed at a recent conference on the so-called Black Swans (i.e. However, the most important flaw is hidden and it is conceptual. Even after a catastrophic event it is difficult to estimate the total damage and cost. Estimation of the costs/consequences of these events. Since this factor multiplies the “cost” in the above equation it is of paramount importance.Ģ. Rare events have very low probabilities and these are extremely difficult to estimate due to the fact that the sample of available data is very small (what is the probability of an event similar to 9/11?). Estimation of probabilities of future events is very difficult (while it is considerably easier when talking of past events). This definition is flawed because of two fundamental reasons, which the formula itself suggests very eloquently:ġ. Risk = the Probability of something happening X resulting Cost/Consequences Probably the most frequently used definition of risk is this one: The display (used in the display element of a Coding).Your preferred source of resilience information
#Ffx hi risk probability code#
The code (used as the code in the resource instance) The source of the definition of the code (when the value set draws in codes defined elsewhere) In this scheme, some codes are under other codes, and imply that the code they are under also applies The specified outcome is effectively guaranteed.Įxplanation of the columns that may appear on this page:Ī few code lists that FHIR defines are hierarchical - each code is assigned a level. The specified outcome is more likely to occur than not. The specified outcome has a reasonable likelihood of occurrence. The specified outcome is possible but unlikely. The specified outcome is exceptionally unlikely. Expansion based on Risk Probability v0.1.0 (CodeSystem)Īll codes in this table are from the system Code


 0 kommentar(er)
0 kommentar(er)
